面试题03.数组中重复的数字
找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

思路一:
因为数组里的数字都在0~n-1的范围内,因此我们令每个数字到它对应的下标,如nums[1] = 1这样。最后如果得到nums[i] == nums[nums[i]]即出现重复值,返回即可。(注:该思路能成的条件是题目中提到的“所有数字都在 0~n-1 的范围内”)
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
for(int i = 0; i < nums.size(); ++i) {
while(i != nums[i]) {
if(nums[i] == nums[nums[i]])
return nums[i];
swap(nums[i], nums[nums[i]]);
}
}
return 0;
}
};
思路二:先对数组进行排序,然后从头扫描数组并判断其是否与其前面相邻元素相等。如果是,返回结果即可。
解题思路三:利用哈希表查找
创建一个集合,然后依次扫描数组中元素,如果数组中的元素不在集合中,将其加入集合;如果已在集合中,说明该元素重复出现,将其作为结果返回。
面试题04.二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:

给定 target = 5,返回 true。
给定 target = 20,返回 false。
限制:
0 <= n <= 1000
0 <= m <= 1000
思路:从矩阵右上角这个数开始,如果这个数比target大,则往左移一列,如果这个数比target小,则往下移一行。该方法不会错过target(如果有的话)。也可以从矩阵左下角开始,同理可解。
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target)
{
//矩阵为空的时候返回false
if(matrix.size()==0)
{
return false;
}
//右上角开始,行索引值为0,列索引值为最大
int row=0,column=matrix[0].size()-1;
//要在矩阵范围内寻找
while(row<matrix.size()&&column>=0)
{
if(matrix[row][column]==target)
{
return true;
}
else if(matrix[row][column]<target)
{
row++;
}
else if(matrix[row][column]>target)
{
column--;
}
}
return false;
}
};
面试题05.替换空格
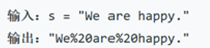
请实现一个函数,把字符串 s 中的每个空格替换成”%20″。
示例:
限制:
0 <= s 的长度 <= 10000
思路:暴力替换
class Solution {
public:
string replaceSpace(string s)
{
for(int i=0;i!=s.size();++i)
{
if(s[i]==' ')
{
s.replace(i,1,"%20");
}
}
return s;
}
};
面试题06. 从尾到头打印链表

思路1:遍历链表,然后将每个节点的值插入到数组的头部。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
vector<int> reversePrint(ListNode* head)
{
vector<int> v;
ListNode *temp=head;
while(temp!=NULL)
{
v.insert(v.begin(),temp->val);
temp=temp->next;
}
return v;
}
};
思路2:栈;递归。
递归的代码:
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
if(!head)
return {};
vector<int> a=reversePrint (head->next);
a.push_back(head->val);
return a;
}
};
class Solution {
public:
vector<int> reversePrint(ListNode* head)
{
vector<int> result;
if(head == NULL)
return result;
help(head,result);
return result;
}
void help(ListNode *node,vector<int>& v)
{
if(node == NULL)
return;
help(node->next,v);
v.push_back(node->val);
}
};
面试题07.重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

思路:用递归的方法。首先要知道,只有前序序列加中序序列或者中序序列加后序序列才能确定一棵唯一的二叉树。

上述两棵二叉树的前序序列和中序序列都为(1,1)。根据二叉树的定义,我们知道这两棵二叉树是不相等的。
根据前序序列和中序序列的性质,我们也能找到方法:先序序列的第一个字符为根节点。对于中序序列,这个根节点在其中间,左边部分是根节点的左子树的中序序列,右边部分是根节点的右子树的中序序列。
先序:abdgcefh –> a bdg cefh
中序:dgbaechf –> dgb a echf
得出结论:a是树根,a有左子树和右子树,左子树有bdg结点,右子树有cefh结点。
先序:bdg –> b dg
中序:dgb –> dg b
得出结论:b是左子树的根结点,b无右子树,有左子树。
先序:dg –> d g
中序:dg –> d g
得出结论:d是b的左子树的根结点,d无左子树,有右子树。
先序:cefh –> c e fh
中序:echf –> e c hf
得出结论:c是右子树的根结点,c有左子树(只有e结点),有右子树(有fh结点)。
先序:fh –> f h
中序:hf –> h f
得出结论:f是c的左子树的根结点,f有左子树(只有h结点),无右子树。
还原二叉树为:
a
b c
d e f
g h
由此,我们可以写出代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
if(preorder.size()==0||inorder.size()==0) //当序列为空时
{
return NULL;
}
return build(preorder,inorder);
}
TreeNode* build(vector<int>& pOrder,vector<int>& iOrder)
{
TreeNode* node=new TreeNode;
node->val=pOrder[0];
node->left=NULL;
node->right=NULL;
int rootNode=pOrder[0]; //获取(子)树的根节点
int index;
for(int i=0;i<iOrder.size();++i) //获取根节点在中序序列中的索引值
{
if(iOrder[i]==rootNode)
{
index=i;
break;
}
}
//左子树中序序列
vector<int> lchildInorder;
int lchildLength=0; //长度
for(int i=0;i<index;++i)
{
lchildInorder.push_back(iOrder[i]);
lchildLength++;
}
//右子树中序序列
vector<int> rchildInorder;
int rchildLength=0;
for(int i=index+1;i<iOrder.size();++i)
{
rchildInorder.push_back(iOrder[i]);
rchildLength++;
}
//左子树的前序序列
vector<int> lchildPreorder;
for(int i=1;i<lchildLength+1;++i)
{
lchildPreorder.push_back(pOrder[i]);
}
//右子树的前序序列
vector<int> rchildPreorder;
for(int i=1+lchildLength;i<pOrder.size();++i)
{
rchildPreorder.push_back(pOrder[i]);
}
if(lchildLength>0)
{
//递归
node->left=build(lchildPreorder,lchildInorder);
}
if(rchildLength>0)
{
//递归
node->right=build(rchildPreorder,rchildInorder);
}
return node;
}
};
面试题09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )

示例解释:输入是操作和对应的输入值,比如操作是appendTail 对应的数值可能是数字或[], deleteHead 对应[]。输出一个道理,只有deleteHead有返回值,其余都是null。只要函数正确,不用太关心输入输出也能解题。
思路:入队的时候,将元素压入a栈。出队的时候,如果队列不为空(a栈和b栈不为空),则检查b栈是否为空,如果b栈为空,则将a栈的元素逐个倒入到b栈,再将b栈首个元素弹出,这就完成出队操作;如果b栈不为空,则直接弹出b栈的元素。该方法将b栈作为了一个缓冲区,通过将a栈元素逐个倒入到b栈,让b栈元素出栈的结果与队列相同。
class CQueue
{
public:
stack<int>a;
stack<int>b;
CQueue()
{
}
void appendTail(int value)
{
a.push(value);
}
int deleteHead()
{
//“队列”为空
if(a.empty()&&b.empty())
{
return -1;
}
if(b.empty())
{
//将a栈逐个倒入b栈
while(!a.empty())
{
b.push(a.top());
a.pop();
}
}
//出队
int temp=b.top();
b.pop();
return temp;
}
};
面试题10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项。斐波那契数列的定义如下:
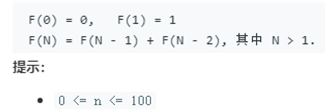
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
思路一:很容易想到用递归的方法:
class Solution {
public:
int fib(int n)
{
if(n==0)
{
return 0;
}
else if(n==1)
{
return 1;
}
else
{
n=fib(n-1)+fib(n-2);
return n%1000000007;
}
}
};
但这个方法的缺点是效率太低了,其时间复杂度为O(n2),每个数都要用同样的函数计算前两个数。
思路二:用三个数first,second和third。每次将first和second的值相加赋给third,然后将second的值赋给first,将third的值赋给second,如此循环。
class Solution {
public:
int fib(int n)
{
if(n==0)
{
return 0;
}
else if(n==1)
{
return 1;
}
else
{
int first=0,second=1;
int third=0;
for(int i=2;i<=n;++i)
{
third=(first+second)%1000000007;
first=second%1000000007;
second=third;
}
return third%1000000007;
}
}
};
时间复杂度为n,空间复杂度为1,很高效。
思路三:用数组来存,求第几项就有多长的数组,前两项的值等于第三项来算,空间复杂度为n,时间复杂度为n。
面试题10- II. 青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。N=0时,输出为1。

思路:设跳上 n 级台阶有 f(n) 种跳法。在所有跳法中,青蛙的最后一步只有两种情况: 跳上 1 级或 2 级台阶。
当为 1 级台阶: 剩 n-1 个台阶,此情况共有 f(n-1) 种跳法;
当为 2 级台阶: 剩 n-2 个台阶,此情况共有 f(n-2) 种跳法。
f(n)为以上两种情况之和,即 f(n)=f(n-1)+f(n-2),以上递推性质为斐波那契数列。本题可转化为求斐波那契数列第n项的值,与面试题10-I.斐波那契数列等价,唯一的不同在于起始数字不同。
青蛙跳台阶问题: f(0)=1,f(1)=1,f(2)=2;
斐波那契数列问题: f(0)=0,f(1)=1,f(2)=1。
class Solution {
public:
int numWays(int n)
{
if(n==0)
{
return 1;
}
else if(n==1||n==2)
{
return n;
}
else
{
int first=1,second=2;
int third;
for(int i=3;i<=n;++i)
{
third=(first+second)%1000000007;
first=second;
second=third;
}
return third;
}
}
};
面试题11. 旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。

思路一:二分法
解题思路:
- 如下图所示,寻找旋转数组的最小元素即为寻找右排序数组的首个元素numbers[x],称x为旋转点。
- 排序数组的查找问题首先考虑使用二分法解决,其可将遍历法的 线性级别 时间复杂度降低至 对数级别。
算法流程:
- 循环二分:设置i,j指针分别指向numbers数组左右两端,m =(i+j)//2为每次二分的中点(“//”代表向下取整除法,因此恒有i≤m<j),可分为以下三种情况:
- 当numbers[m]>numbers[j]时:m一定在左排序数组中,即旋转点x一定在[m+1,j]闭区间内,因此执行 i = m + 1;
- 当numbers[m]<numbers[j]时:m一定在右排序数组中,即旋转点x一定在[i,m]闭区间内,因此执行 j = m;
- 当numbers[m]==numbers[j]时:无法判断m在哪个排序数组中,即无法判断旋转点x在[i,m]还是[m+1,j]区间中。解决方案:执行j=j-1缩小判断范围(分析见以下内容)。
- 返回值:当 i==j 时跳出二分循环,并返回numbers[i]即可。
思考:是否可以用numbers[m]和numbers[i]比较做代替?
解析:不可以。因为做比较的目的是判断m在哪个排序数组中。但在numbers[m]>numbers[i]情况下,无法判断 m 在哪个排序数组中。本质是因为 j 初始值肯定在右排序数组中;i 初始值无法确定在哪个排序数组中。
示例:当 i==0,j==4,m==2 时,有numbers[m]>numbers[i],以下两示例得出不同结果。
numbers==[1,2,3,4,5]旋转点 x==0:m在右排序数组(此示例只有右排序数组);
numbers==[3,4,5,1,2]旋转点 x==3:m在左排序数组。
展开分析numbers[m] == numbers[j]情况:
- 无法判定 m 在左(右)排序数组:设以下两个旋转点值为0的示例数组,则当 i == 0,j == 4 时,m == 2,两示例结果不同。
- 例[1,0,1,1,1]:旋转点 x==1,因此 m==2在右排序数组中。
- 例[1,1,1,0,1]:旋转点 x==3,因此 m==2在左排序数组中。
- i == j – 1 操作的正确性证明:只需证明每次执行此操作后,旋转点x仍在[i,j]区间内即可。
- 若 m 在右排序数组中:numbers[m] == numbers[j],因此数组[m,j](恒有m<j)区间内所有元素值相等,执行j == j – 1只会抛弃一个重复值
- 若 m 在左排序数组中:由于 左排序数组 任意元素 ≥ 右排序数组 任意元素,因此可推出旋转点元素值 numbers[x] ≤ numbers[j] ==numbers[m],则有:
- 若numbers[x] <numbers[j]:即j左方仍有值更小的元素,执行j = j – 1后旋转点x仍在[i,j]区间内。
- 若numbers[x] == numbers[j]:分为以下两种情况:
- 当 j>x:易得执行 j == j – 1后旋转点x仍在[i,j]区间内。
- 当 j == x:特殊情况,即执行 j==j-1后旋转点 x 可能不在[i,j]区间内。例如[1,2,3,2,3,1],当 i = 0,m = 2,j = 5时执行 j = j-1 后虽然丢失了旋转点索引 x = 5,但最终返回值仍正确(最终返回的numbers[0]等于旋转点numbers[5]),这时因为:之后的二分循环一直在执行 j = m,而区间[i,m]内元素值一定都等于旋转点值numbers[x] (因为区间内元素值既要满足≥也要满足≤numbers[x]),因此仍可保证正确的返回值。
总结:此方法可以保证返回值 numbers[i] 等于旋转点值 numbers[x];但在少数特例下 i 不是旋转点 x。本题目只要求返回“旋转点的值”,因此本方法可行。
class Solution {
public:
int minArray(vector<int>& numbers)
{
int i=0,j=numbers.size()-1;
while(i<j)
{
int m=(i+j)/2;
if(numbers[m]>numbers[j]) //m一定在左序列
{
i=m+1;
}
else if(numbers[m]<numbers[j]) //m一定在右序列
{
j=m;
}
else //m==j时
{
j--;
}
}
return numbers[i];
}
};
思路二:遍历法,当遍历到的数大于后一个数,则后一个数为最小元素。如果没找到,则第一个数为最小元素。
class Solution {
public:
int minArray(vector<int>& numbers)
{
int count=numbers.size();
for(int i=0;i<count-1;i++)
{
if(numbers[i]>numbers[i+1])
{
return numbers[i+1];
}
}
return numbers[0];
}
};
面试题12. 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
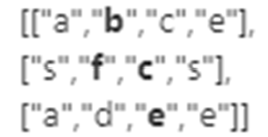
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。

思路:深度优先搜索+剪枝。深度优先搜索一般用递归实现。
算法原理:
- 深度优先搜索:可以理解为暴力法遍历矩阵中所有字符串可能性。DFS通过递归,先朝一个方向搜到底,再回溯至上个节点,沿另一个方向搜索,以此类推。
- 剪枝:在搜索中,遇到 这条路不可能和目标字符串匹配成功 的情况(例如:此矩阵元素和目标字符不同、此元素已被访问),则应立即返回,称之为 可行性剪枝。
算法剖析:
- 递归参数:当前元素在矩阵 board 中的行列索引 i 和 j ,当前目标字符在 word 中的索引 k 。
- 终止条件:
- 返回 false:① 行或列索引越界 或 ② 当前矩阵元素与目标字符不同 或③ 当前矩阵元素已被访问过(③可合并至②)。
- 返回true:字符串 word 已全部匹配,即 k=len(word) – 1 。
- 递推工作:
- 标记当前矩阵元素:将 board[i][j] 值暂存与变量 temp ,并修改字符为空‘ ’,代表此元素已被访问过,防止之后搜索时重复访问。
- 搜索下一单元格:朝当前元素的 上、下、左、右 四个方向开启下层递归,使用 或 连接(代表只需一条可行路径),并记录结果至 result 。
- 还原当前矩阵元素:将 temp 暂存值还原至 board[i][j] 元素。
- 回溯返回值:返回 result ,代表是否搜索倒目标字符串。
复杂度分析:
M,N分别为矩阵行列大小,K为字符串 word 长度。
- 时间复杂度O(3^k·MN):最差情况下,需要遍历矩阵中长度为K字符串的所有方案,时间复杂度为O(3^k);矩阵中共有MN个起点,时间复杂度为O(MN)。
- 方案数计算:设字符串长度为K,搜索中每个字节有上下左右四个方向可以选择,舍弃回头(上个字符)的方向,剩下3种选择,因此方案数的复杂度为O(3^k)。
- 空间复杂度O(K):搜索过程种的递归深度不超过K,因此系统因函数调用累计使用的栈空间占用O(K)(因为函数返回后,系统调用的栈空间会释放)。最坏的情况下K = MN,递归深度为MN,此时系统栈使用O(MN)的额外空间。
class Solution {
public:
bool exist(vector<vector<char>>& board, string word)
{
if(board.size()==0||word.size()==0)
{
return false;
}
else
{
//从左上角开始一个个执行算法
for(int i=0;i<board.size();++i)
{
for(int j=0;j<board[0].size();++j)
{
if(dfs(board,word,i,j,0))//从word[0]开始
return true;
}
}
return false;
}
}
bool dfs(vector<vector<char>>& board,string word,int x,int y,int k)
{
//如果越界或者不是下一个字符
if(x<0||x>=board.size()||y<0||y>=board[0].size()||board[x][y]!=word[k])
return false;
if(k==word.size()-1)//如果是最后一个字符了
return true;
//如果要不是最后一个字符,继续递归,将走过的字符设置为空,表示不能再进入了
char temp=board[x][y];
board[x][y]=' ';
//递归,以下、上、右、左方向深度优先搜索,如果有某个函数返回了true
//则直接给result赋值为true,不会执行后面的函数,实现剪枝节约时间
bool result=dfs(board,word,x+1,y,k+1)||dfs(board,word,x-1,y,k+1)||
dfs(board,word,x,y+1,k+1)||dfs(board,word,x,y-1,k+1);
//恢复刚才设置为空的格子
board[x][y]=temp;
return result;
}
};
面试题13.机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?

思路:
本体与“矩阵中的路径”类似,是典型的矩阵搜索问题。此类问题通常可使用 深度优先搜索DFS 或 广度优先搜素BFS 解决。在介绍DFS/BFS算法之前,为提升计算效率,首先讲述两项前置工作:数位之和计算、搜索方向简化。
数位之和计算:
- 设一数字x,向下取整除法符号 // ,求余符号⊗,则有:
- x⊗10:得到x的个位数字;
- x //10:令x的十进制数向由移动一位,即删除个位数字。
- 因此,可通过循环求得数位和,数位和计算的封装函数如下所示:
int sum(int x)//计算位数和
{
int res=0;
while(x>0)
{
res+=x%10;
x=x/10;
}
return res;
}
搜索方向简化:
- 数位和特点:根据数位和增量公式得知,数位和每逢 进位 突变一次。
- 解的三角形结构:
- 根据数位和特点,矩阵中 满足数位和的解 构成的几何形状如多个 等腰直角三角形,每个三角形直角顶点位于0,10,20,……等数位和突变的矩阵索引处。
- 三角形内的解虽然都满足数位和要求,但由于机器人每步只能走一个单元格,而三角形间不一定是连通的,因此机器人不一定能到达,称之为 不可达解;同理,可到达的解称为 可达解(本体求此解)。
- 结论:根据可达解的结构,易推出机器人可 仅通过向下和向右移动,访问所有可达解。
- 三角形内部:全部联通,易证;
- 两三角形连通处:若某三角形内的解为可达解,则必与其左边或上边的三角形连通(即相交),即机器人必可从左边或上边走进此三角形。
深度优先遍历DFS
- 深度优先搜索:可以理解为暴力法模拟机器人在矩阵中的所有路径。DFS通过递归,先朝一个方向搜倒底,再回溯至上个节点,沿另一个方向搜索,以此类推。
- 剪枝:在搜索中,遇到数位和超出目标值、此元素已访问,则应立即返回,称之为可行性剪枝。
算法解析:
- 递归参数:当前元素在矩阵种的行列所有 i 和 j ,行数 m ,列数 n ,k 值以及访问矩阵 visited。
- 终止条件:当 ① 行列索引越界 或 ② 数位和超出目标值 k 或 ③ 当前元素已访问过的时候,返回0,代表不计入可达解。
- 递推工作:
- 标记当前单元格:将索引 (i,j)存入 visited 种,代表此单元格已被访问过。
- 搜索下一单元格:计算当前元素的 下、右 两个方向元素的位数和,并开启下层递归。
- 回溯返回值:返回 1+右方搜索的可达解总数 + 下方搜索的可达解总数,代表从本单元格递归搜索的可达解总数。
复杂度分析:
M,N分别为矩阵行列大小。
- 时间复杂度 O(MN):最差情况下,机器人遍历矩阵所有单元格,此时时间复杂度为O(MN)。
- 空间复杂度 O(MN):最差情况下,visited 内存储矩阵所有单元格的索引,使用O(MN)的额外空间。
class Solution {
public:
int sum(int x)//计算位数和
{
int res=0;
while(x>0)
{
res+=x%10;
x=x/10;
}
return res;
}
int movingCount(int m, int n, int k)
{
//申请记录数组,m行,n列
vector<vector<bool>> visited(m,vector<bool> (n));
//从左上角开始
return dfs(0,0,m,n,k,visited);
}
//参数列表为行坐标,列坐标,m,n,k,已被访问数组
int dfs(int i,int j,int m,int n,int k,vector<vector<bool>>& visited)
{
//如果越界或位数和大于k或已被访问
if(i>=m||j>=n||sum(i)+sum(j)>k||visited[i][j])
return 0;
visited[i][j]=true;
return 1+dfs(i+1,j,m,n,k,visited)+dfs(i,j+1,m,n,k,visited);
}
};
面试题14- I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m] 。请问 k[0]*k[1]*…*k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。

思路:贪心
设一绳子长度为 n(n>1),则其必可被切分为两段 n=n1+n2;
根据经验推断,切分的两数字乘积往往比原数字更大,即往往有
n1×n2>n1+n2 = n
- 例如绳子长度为 6 :6 =3 + 3 小于 3 × 3 = 9;
- 也有少数反例,例如 2 :2 = 1 + 1 > 1 × 1 = 1。
推论一:合理的切分方案可以带来更大的乘积。
设一绳子长度为 n (n>1),切分为两段 n = n1 + n2,切分为三段
n = n1 + n2 + n3。
根据经验推断,三段 的乘积往往更大,即往往有 n1n2n3 > n1n2。
- 例如绳子长度为 9 :两端 9 = 4 + 5 和三段 9 = 3 + 3 + 3则有
4 × 5 < 3 × 3 × 3 。 - 也有少数反例,例如6 :两段 6 = 3 + 3 和三段6 = 2 + 2 + 2,
则有 3 × 3> 2 × 2 × 2。
推论二:若切分方案合理,绳子段切分得越多,乘积越大。
总体上看,貌似长绳子切分为越多段乘积越大,但其实倒某个长度分界点后,乘积到达最大值,就不应再切分了。
问题转化:是否有优先级最高的长度 x 的存在?若有,则应该尽可能把绳子以 x 长度切为多段,以获取最大乘积。
推论三:为使乘积最大,只有长度为 2 和 3 的绳子不应再切分,且 3 比 2 更优(详情见下表)。
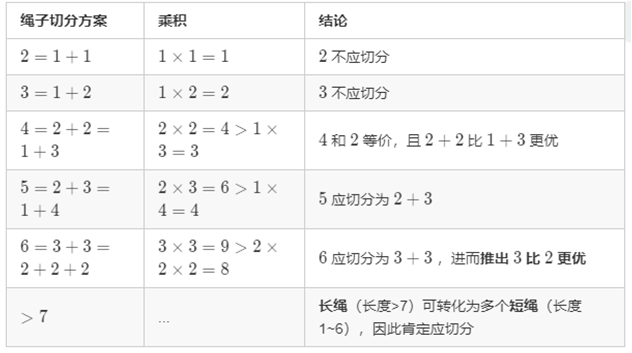
class Solution {
public:
int cuttingRope(int n)
{
if(n<=3)
return n-1;
if(n%3==0)//可以全分为长为3的
return pow(3,n/3);//返回3的n/3次方
if(n%3==1)//全分为3多了1
return pow(3,n/3-1)*2*2;
//全分为3多了2
return pow(3,n/3)*2;
}
};
当n为2或3时,由于m>1,必须至少要剪成两段,因此它们的答案是n-1
当n可以分成全部长度是3时,就全分为3
当n全分为3还剩下长度为1的绳子,则把最后的3+1变成2+2
当n全分为3还剩下长度为2的绳子,则保持不变
面试题14- II. 剪绳子 II
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m] 。请问 k[0]*k[1]*…*k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。

思路:与上一题剪绳子Ⅰ主体思路相同,但这道题由于n的范围变大,要考虑到大数越界的情况。我们可以分步乘积,每次乘积取模。
class Solution {
public:
int cuttingRope(int n)
{
if(n<=3)
return n-1;
long res=1;
while(n>4)
{
res=(res*3)%1000000007;
n=n-3;
}
return res*n%1000000007;
}
};
对n>4的说明:有三种(余数)情况判断为false,分别是n-3=4,3,2,
当余数n=4时,分为2*2=4,结果res直接乘n;
当余数n=3时,3最优,res*n;
当余数n=2时,2不再拆分成1*1,直接*n。最后别忘了返回前再取模一次
面试题15. 二进制中1的个数
请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。

题目描述得与实例输入有区别,其实输入的是十进制数。
思路一:逐位相与,用二进制右移辅助。
- 根据 与运算 定义,设二进制数字 n,则有:
- 若 n & 1 = 0,则 n 二进制 最右一位 为0;
- 若 n & 1 = 1,则 n 二进制 最右一位 为1。
- 根据以上特点,考虑以下 循环判断:
- 判断 n 最右一位是否为 1 ,根据结果计数。
- 将 n 右移一位 (本体要求把数字 n 看作无符号数,因此使用 无符号右移 操作)。
class Solution {
public:
int hammingWeight(uint32_t n)
{
int res=0;
while(n!=0)
{
if((n&1)==1)
res++;
n=n>>1;
}
return res;
}
};
n == 0时,说明已经没有 1 了,此时跳出循环。
当低位为 1 ,res++,然后n向右移一位,舍弃掉最低一位。
不管最低位是不是 1 ,都要右移。
思路二:用 n & (n-1),不用右移。
- (n-1)解析:二进制数字 n 最右边的 1 变成 0,此 1 右边的 0 都变成 1。
- n &(n-1)解析:二进制数字 n 最右边的 1 变成 0 ,其余不变。

因此 n &(n-1)相当于把最右边的 1 变为 0。
class Solution {
public:
int hammingWeight(uint32_t n)
{
int res=0;
while(n!=0)
{
res++;
n=n&(n-1);
}
return res;
}
};
复杂度分析:
- 时间复杂度O(M):n &(n-1)操作仅有减法和与运算,占用O(1);设M为二进制数字 n 种 1 的个数,则需循环M次(每轮消去一个1),占用O(M)。
- 空间复杂度O(1):变量 res 使用常数大小额外空间。
面试题16. 数值的整数次方
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。

思路一:用循环一个个相乘,但这样在指数很大的时候比较慢。
思路二:快速幂。
快速幂法 可将时间复杂度降低至O(log2n)

class Solution {
public:
double myPow(double x, int n)
{
if(x==0.0)
return 0.0;
if(n==0)
return 1.0;
long a=n;
double res=1.0;
if(a<0)
{
x=1/x;
a=-a;
}
while(a>0)
{
if((a&1)==1) //当二进制最后位为1
res=res*x;
x=x*x;//二进制,右移一位后加1次方
a=a>>1;//右移一位
}
return res;
}
};
代码里用长整型long变量a来代替n,因为测试用例中有一项n的值超出了整型int的范围。
面试题17. 打印从1到最大的n位数
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。

思路:很容易想到,当n=1时,从1开始打印到10(不包括10),当n=2时,从1开始打印到100(不包括100),当n=3时,从1开始打印到1000(不包括1000),因此范围上限为10的n次方,开区间。
class Solution {
public:
vector<int> printNumbers(int n)
{
vector<int> res;
int len=pow(10,n);
for(int i=1;i<len;++i)
{
res.push_back(i);
}
return res;
}
};
面试题18. 删除链表的节点
给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。(此题对《剑指offer》原题有改动)

思路:这是一道常规的删除单链表节点的题,但这道题没有头结点,如果直接做,需要单独考虑当需要删除的节点为第一个节点时,和当链表只剩下一个节点——并要删除该节点的情况,这样就导致了需要分不同情况。
为了让情况更加统一化,我们可以给链表增加一个头结点,这里称为哑结点(dummyNode),之后对链表的删除操作就很方便了。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val)
{
ListNode* dummyhead=new ListNode(1);
dummyhead->next=head;//将哑节点连接到链表首部
ListNode *cur=dummyhead;//cur节点从哑节点开始
while(cur!=NULL&&cur->next!=NULL)
{
if(cur->next->val==val)//cur指向的是被删除节点的前一个节点
{
cur->next=cur->next->next;
}
cur=cur->next;
}
return dummyhead->next;
}
};
在《剑指offer》上,这道题是这样的:给一个链表头指针和指向要删除节点的指针,在O(1)系统时间内删除该节点。
思路:既然节点指针指向的是要被删除的节点delete,所以我们无法拿到它的上一个节点,但是,我们可以利用该节点的下一个节点next:将下一个节点next的val赋值给要删除的节点delete,然后删除下一个节点next,就完成了。
但这个方法仍然有其他情况:
如果被删除的节点是最后一个,无法拿到下一个节点next,我们就只能从头顺序遍历到它的前序节点来删除。如果链表中只有一个节点,那删除后要把头指针设置为null。
面试题20. 表示数值的字符串

先去除字符串首尾的空格,然后根据e划分指数和底数,再判断指数和底数是否合法即可。
class Solution {
public:
bool isNumber(string s) {
//1、从首尾寻找s中不为空格首尾位置,也就是去除首尾空格
int i=s.find_first_not_of(' ');
if(i==string::npos)return false;
int j=s.find_last_not_of(' ');
s=s.substr(i,j-i+1);
if(s.empty())return false;
//2、根据e来划分底数和指数
int e=s.find('e');
//3、指数为空,判断底数
if(e==string::npos)return judgeP(s);
//4、指数不为空,判断底数和指数
else return judgeP(s.substr(0,e))&&judgeS(s.substr(e+1));
}
bool judgeP(string s)//判断底数是否合法
{
bool result=false,point=false;
int n=s.size();
for(int i=0;i<n;++i)
{
if(s[i]=='+'||s[i]=='-'){//符号位不在第一位,返回false
if(i!=0)return false;
}
else if(s[i]=='.'){
if(point)return false;//有多个小数点,返回false
point=true;
}
else if(s[i]<'0'||s[i]>'9'){//非纯数字,返回false
return false;
}
else{
result=true;
}
}
return result;
}
bool judgeS(string s)//判断指数是否合法
{
bool result=false;
//注意指数不能出现小数点,所以出现除符号位的非纯数字表示指数不合法
for(int i=0;i<s.size();++i)
{
if(s[i]=='+'||s[i]=='-'){//符号位不在第一位,返回false
if(i!=0)return false;
}
else if(s[i]<'0'||s[i]>'9'){//非纯数字,返回false
return false;
}
else{
result=true;
}
}
return result;
}
};
面试题21. 调整数组顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。

思路一:用首尾指针left和right来交换奇偶数。
这个思路最开始踩了一个坑,就是在left和right指针的基础上,left指向左边奇数数组的最后一位,right指向右边偶数数组的第一位,然后用索引i来遍历数组,将nums[i]与nums[++left]或者nums[- -right]交换。这个方法不是不行,但是实现起来,要考虑最开始,并没有奇数数组或者偶数数组,而且交换的过程可能有重复交换(奇数与奇数交换,偶数与偶数交换),如果要提高效率需要再单独判断与奇偶不同的数交换。因此用索引i来遍历显得很蠢。
后来,我发现直接用两个指针来遍历更加方便:当left指向的是奇数,则向后移动,若指向的是偶数,则与right的值交换;当right指向的是偶数,则向前移动,若指向的是奇数,则于left的值交换;当left于right相等时跳出循环。
class Solution {
public:
vector<int> exchange(vector<int>& nums)
{
if(nums.size()==0)
return nums;
//左右指针,用来交换数组中的数
int left=0;
int right=nums.size()-1;
while(left<right)
{
if(nums[left]%2==1)
{
left++;
}
else if(nums[left]%2==0)
{
swap(nums[left],nums[right]);
}
if(nums[right]%2==0)
{
right--;
}
else if(nums[right]%2==1)
{
swap(nums[right],nums[left]);
}
}
return nums;
}
};
有改良版算法:left搜索偶数的位置,然后停下来,right搜索奇数的位置,然后停下来,再交换二者的值。
思路二:快慢指针。
快指针fast,慢指针low。它们都从左往右遍历数组,慢指针low在遇到偶数时停下来,然后快指针fast继续往前(从慢指针low的位置开始),搜索奇数,搜索到之后交换它们的值,之后慢指针low向前移动一位。在快指针搜索完最后一个元素也没发现奇数时,说明调整完毕,跳出循环。
面试题22. 链表中倒数第k个节点
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。例如,一个链表有6个节点,从头节点开始,它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。
思路一:计算返回节点。
要想通过k来计算应该返回第几个节点,首先要知道链表的长度。可是该题没有告知链表长度,所以如果一定要用这个方法,就要先从头到尾遍历一遍链表,得到长度len,然后返回第(len-k)+1个节点。但这个方法太浪费时间了,运气最差会有O(n2)时间复杂度。
思路二:双指针(快慢指针)。
核心思想是,快指针fast在前,慢指针low在后,它们保持着一定距离一起向前遍历,当快指针fast遍历结束后,通过慢指针low来返回节点。
知道了核心思想,下面来讨论该如何得出最合适的距离和什么时候fast结束遍历:
最直观的,快指针先比慢指针多执行k次(fast=fast->next)的操作,然后再一起向前遍历,直到快指针在最后一个节点处停下,经过观察,需要返回low指针的下一个节点。但这里有一个缺陷,就是当k等于链表长度时,快指针在初始化后会指向最后一个节点的next域即NULL,如果在后面判断快指针是否指向最后一个节点条件是这样写的(fast->next!=NULL),那这里就会出现空指针的情况,会报错。
为了解决这个问题,我们可以在初始化快指针fast的位置时,只执行k-1次的(fast=fast->next)操作,最后返回low指针指向的节点。
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k)
{
//快慢指针
ListNode* low=head;
ListNode* fast=head;
//将快指针放到开始的位置
for(int i=0;i<k-1;++i)
{
fast=fast->next;
}
while(fast->next!=NULL)
{
fast=fast->next;
low=low->next;
}
return low;
}
};
面试题24. 反转链表
定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。

思路一:用额外空间,比如申请一个新的arraylist或者链表,从头插入,然后输出。但这样百分百会被面试官问还有没有更优解。
思路二:用双指针。
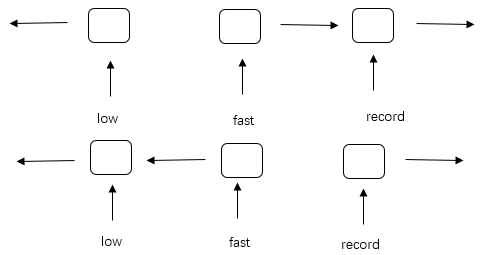
如果原地反转链表,则要将后面一个节点的next域指向前一个节点,这就需要两个指针low和fast。但问题来了,如果后一个节点的next不再指向原链表的下一个节点,那链表就此断开,算法就无法继续了。因此我们还需要一个指针record,用来指向fast指针指向的节点的下一个节点。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head)
{
if(head==NULL)
{
return NULL;
}
ListNode* low=NULL;
ListNode* fast=head;
ListNode* record=head->next;
//record指向null时跳出
while(record!=NULL)
{
//反转链表
fast->next=low;
//移动指针
low=fast;
fast=record;
record=record->next;
}
fast->next=low;//别忘了跳出时还有一步没做完
return fast;
}
};
面试题25. 合并两个排序的链表
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。

思路一:暴力遍历。
先判断是否有链为空,特殊处理。
增加头结点,方便操作。
用两个指针cur1和cur2分别遍历l1和l2。cur1用来找插入点,cur2用来找插入值。因为两个链表都是递增排序的,只要l1有节点比l2的节点大了(等于也算),说明找到了插入点和插入值,否则,则继续找。当l1最后一个节点都比l2的某一个节点小了,可以直接把剩下的l2节点接到l1尾部。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
{
//首先判断是否有链为空
if(l1==NULL)
{
return l2;
}
else if(l2==NULL)
{
return l1;
}
else if(l1==NULL&&l2==NULL)
{
return NULL;
}
//加入头节点
ListNode* head1=new ListNode(-1);
ListNode* head2=new ListNode(-1);
head1->next=l1;
head2->next=l2;
//加入头指针
ListNode* cur1=head1;
ListNode* cur2=head2->next;
while(cur2!=NULL)
{
//当l1最后一位节点都比l2某一位节点小
//直接把l2当前节点与它后面的节点接过来
if(cur1->next==NULL)
{
cur1->next=cur2;
break;
}
//当l2有节点比cur1下一个节点小,说明该插入了
else if((cur1->next->val)>=(cur2->val))
{
ListNode* temp=new ListNode(cur2->val);
temp->next=cur1->next;
cur1->next=temp;
cur1=cur1->next;
cur2=cur2->next;
}
//如果l2这个节点比cur1下一个节点大,不该插入,往后找插入点
else
{
cur1=cur1->next;
}
}
return head1->next;
}
};
这里是将l2中的节点插入到l1中,也可以单独另起一个链表,将判断后的节点存入新链表,最后返回新链表。
思路二:和上面讲的差不多,因为链表节点是升序排列,所以链表的第一个节点是该链表最小的,就比较链表们的第一个节点,哪个小,就选哪个加入新链表,然后将被选链表的首结点往后移。
其他思路:递归分治和优先队列(堆排序)ORZ。
递归:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if (l1 == NULL) {
return l2;
}
if (l2 == NULL) {
return l1;
}
if (l1->val <= l2->val) {
l1->next = mergeTwoLists(l1->next, l2);
return l1;
}
l2->next = mergeTwoLists(l1, l2->next);
return l2;
}
};
面试题26. 树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。

返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。

思路:递归遍历判断。
取母树为A,子树为B,需要判断B是否为A的子结构。
我们可以一次遍历A中的所有节点,对每个在A中遍历到的节点依次做判断,判断该节点是否可以作为子结构的B的根节点。
在代码中,我们写两个函数:
isSubStructure(),用于遍历A中的所有节点,并调用helper()进行判断
helper(),用于判断A中当前节点能否作为B的根节点
isSubStructure():
先序遍历A中所有节点
如果当前节点为NULL或者B为NULL,返回false。(约定空树不是子结构)
helper():
先序遍历A和B
如果B==NULL,说明B已遍历完,返回true
如果A==NULL,B != NULL,说明A中节点不足以构成子结构B,返回false
如果A->val != A->val,不满足节点值相等条件,返回false。
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B)
{
if(A==NULL||B==NULL)
{
return false;
}
return helper(A,B) || isSubStructure(A->left,B) || isSubStructure(A->right,B);
}
bool helper(TreeNode* A,TreeNode* B)
{
if(B==NULL)//说明遍历完B,找完了子结构
{
return true;
}
else if(A==NULL)//说明遍历完A还没有找完子结构
{
return false;
}
else if(A->val!=B->val)//说明不匹配
{
return false;
}
return helper(A->left,B->left) && helper(A->right,B->right);
}
};
面试题27. 二叉树的镜像
请完成一个函数,输入一个二叉树,该函数输出它的镜像。

思路一:递归(dfs)。从根节点开始,搜索到底,交换节点,然后返回上一节点。
递归终止条件:当节点等于NULL;(节点为叶子节点);交换完毕后
注意:交换节点时,如果只交换节点中的val,那结果是错误的。因为在两个节点翻转时,它们的子结点仍要跟着它们,因此可以把交换节点的动作看作是交换两个指针(left和right)。
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root)
{
if(root==NULL)
{
return NULL;
}
return helper(root);
}
TreeNode* helper(TreeNode* node)
{
if(node==NULL)
{
return NULL;
}
//if(node->right==NULL && node->left==NULL)
//{
//return node;
//}//其实可以免去这两行代码,反正两个叶子节点的子结点null交换后还是null
helper(node->left);
helper(node->right);
//swap(node->left->val,node->right->val);
//交换节点的值得到的不是镜像二叉树
//需要交换左右指针
TreeNode* temp=node->left;
node->left=node->right;
node->right=temp;
return node;
}
};
- 时间复杂度O(N):其中 N 为二叉树的节点数量,建立二叉树镜像需要遍历树的所有节点,占用O(N)时间。
- 空间复杂度O(N):最差情况下(当二叉树退化为链表),递归时系统需使用O(N)大小的栈空间。
面试题28. 对称的二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。

做这道题前,我们要先知道这道题的规律:
对称二叉树中,对于树的任意两个对称节点L和R,一定有:
- L.val = R.val:即此两对称点值相等。
- L.left.val = R.right.val:即L的左子节点和R的右子节点对称;
- L.right.val = R.left.val:即L的右子结点和R的左子节点对称。
思考一下,是不是我们只需要对比上述的值就能够判断该树是不是对称的了呢?
知道了这个规律,我们就有解题方法了。
思路一:递归(dfs)
首先,递归函数的参数:
两个要比较的节点a、b。
跳出条件:
当a、b都为空,也是对称的,返回true;
当a、b其中一个为空,不是对称的,返回false;
当a、b的val不相等,不是对称的,返回false。
然后,递归调用函数,实参就是上述规律的节点。
class Solution {
public:
bool isSymmetric(TreeNode* root)
{
if(root==NULL)
{
return true;
}
return helper(root->left,root->right);
}
bool helper(TreeNode* a,TreeNode* b)
{
//当a、b都为空,对称,返回true
if(a==NULL && b==NULL)
{
return true;
}
//其中一个为空,不对称
if(a==NULL || b==NULL)
{
return false;
}
//值不相同,不对称
if(a->val!=b->val)
{
return false;
}
//比较两个结点的子结点
return helper(a->left,b->right) && helper(a->right,b->left);
}
};
时间复杂度:O(n),因为我们遍历整个输入树一次,所以总的运行时间为O(n),其中n是树中结点的总数。
空间复杂度:递归调用的次数受树的高度限制。在最糟糕情况下,树是线性的,其高度为O(n)。因此,在最糟糕的情况下,由栈上的递归调用造成的空间复杂度为O(n)。
思路二:迭代法(bfs)
该算法的工作原理类似于BFS,但存在一些关键差异。
每次提取两个节点并比较,然后将两个节点的左右子节点按相反的顺序插入队列中。
当队列为空时,或者检测到树不对称时算法结束。
class Solution {
public:
bool isSymmetric(TreeNode* root)
{
if(root==NULL)
{
return true;
}
queue<TreeNode*> q;
q.push(root->left);
q.push(root->right);
while(!q.empty())
{
//队首两个节点出队
TreeNode* a=q.front();
q.pop();
TreeNode* b=q.front();
q.pop();
//两个节点都为空,继续循环
if(a==NULL && b==NULL)
{
continue;
}
//其中一个节点为空
if(a==NULL || b==NULL)
{
return false;
}
//两个节点的值不等
if(a->val!=b->val)
{
return false;
}
//将两个节点的子结点入队
//注意入队的顺序
q.push(a->left);
q.push(b->right);
q.push(a->right);
q.push(b->left);
}
return true;
}
};
复杂度分析
- 时间复杂度:O(n),因为我们遍历整个输入树一次,所以总的运行时间为O(n),其中n是树中节点的总数。
- 空间复杂度:搜索队列需要额外的空间。在最糟糕的情况下,我们不得不向队列中插入O(n)个节点。因此,空间复杂度O(n)。
面试题29. 顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。

思路:模拟、设定边界。
顺时针打印矩阵的顺序是:从左向右、从上向下、从右向左、从下向上循环。
因此我们可以跟着这个顺序走,在走完一行或一列时,缩小矩阵的边界。
空值处理:当matrix为空时,返回空列表[]。
初始化:矩阵上、右、下、左四个边界,up、right、down、left,用于打印的结果列表res。
循环打印:按照上述四个方向循环,每个方向打印中做以下三件事:1.根据边界打印,即将元素按顺序添加至res尾部;2.边界向内收缩1(代表已被打印);3.判断是否打印完毕(边界是否越界),若打印完毕则跳出。
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix)
{
vector<int> res;
if(matrix.empty())
{
return res;
}
//初始化模拟边界值
int up=0;
int right=matrix[0].size()-1;
int down=matrix.size()-1;
int left=0;
while(true)
{
//从左到右遍历
for(int i=left;i<=right;++i)
{
res.push_back(matrix[up][i]);
}
up++;
if(up>down)//如果越界(打印完毕)
{
break;
}
//从上到下遍历
for(int i=up;i<=down;++i)
{
res.push_back(matrix[i][right]);
}
right--;
if(right<left)
{
break;
}
//从右到左遍历
for(int i=right;i>=left;--i)
{
res.push_back(matrix[down][i]);
}
down--;
if(down<up)
{
break;
}
//从下到上遍历
for(int i=down;i>=up;--i)
{
res.push_back(matrix[i][left]);
}
left++;
if(left>right)
{
break;
}
}
return res;
}
};
为什么判断越界的符号不是等于号:当两个边界相等的时候,说明还有一列(行)没有打印。
面试题30. 包含min函数的栈
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。

这题的难点在于如何将min函数的时间复杂度也降到O(1)上。
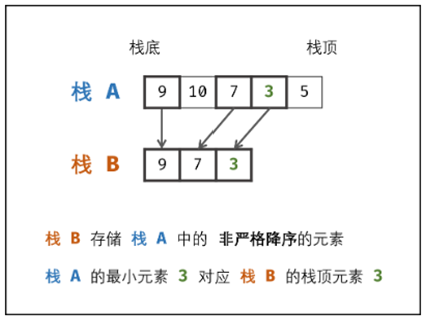
思路:使用两个栈,一个栈用来正常地存储数据,完成push,pop,top等逻辑功能,另一个栈用来存储正常栈中所有非严格降序的元素,完成min功能。
class MinStack {
public:
/** initialize your data structure here. */
//数据栈
stack<int> number;
//small栈
stack<int> small;
MinStack()
{
}
void push(int x)
{
number.push(x);
if(small.empty())//第一个元素
{
small.push(x);
}
else if(x<=small.top())//该元素比最小元素还小(等于也要算)
{
small.push(x);
}
}
void pop()
{
if(!number.empty())
{
//当数据栈弹出的元素和small栈栈顶元素相同,small栈也要弹出
if(number.top()==small.top())
{
number.pop();
small.pop();
}
else
{
number.pop();
}
}
}
int top()
{
return number.top();
}
int min()
{
return small.top();
}
};
对push函数中,x<=small.top()中等于号的解释:为什么等于的时候也要加入small栈,乍一看好像多增加了一次操作——但要注意,数据栈的元素是可以重复的,当重复的元素是最小值,在执行参数为最小值的pop函数时,两个栈都要弹出最小值;而如果因为没加等号,small栈里只有一个最小值元素,弹出后之前重复的最小值在small栈里就没有了(而在数据栈里还有它),会导致错误。








