排序算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度	空间复杂度	是否稳定
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	是
选择排序	O(n²)	O(n)	O(n²)	O(1)	不是
插入排序	O(n²)	O(n)	O(n²)	O(1)	是
快速排序	O(nlog₂n)	O(nlog₂n)	O(n²)	O(log₂n)	不是
归并排序	O(nlog₂n)	O(nlog₂n)	O(nlog₂n)	O(n)	是
堆排序	O(nlog₂n)	O(nlog₂n)	O(nlog₂n)	O(1)	不是

冒泡排序

从前往后遍历数组n次（n为数组长度），每次遍历完后，数组的乱序序列中最大的数将被放在数组乱序序列末尾。
下图中灰色的数为乱序，橙色的数为有序，它们分别组成乱序序列和有序序列。

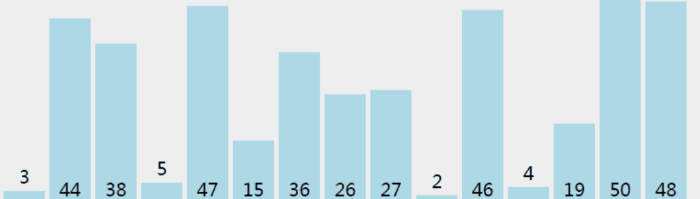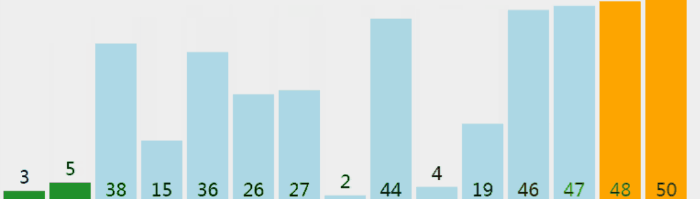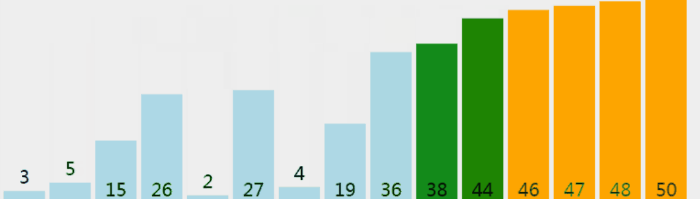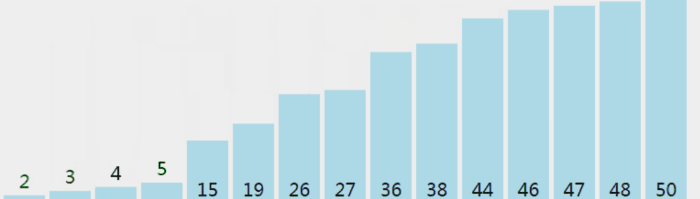
void BubbleSort(int arr[],int len)
{
	for (int i = 0; i < len - 1; ++i)
	{
		for (int j = 0; j < len - 1 - i; ++j)
		{
			if (arr[j] > arr[j + 1])
				swap(arr[j], arr[j + 1]);
		}
	}
}

• 变量len为数组元素个数
• 因为要将当前遍历到的元素与其后面的元素比较，为了防止arr[j+1]越界，内层循环 j < len – 1，多减1
• 内层循环中，后面i个元素是已经排好序的，再次遍历没有意义，因此 j – i 提前退出循环

---

选择排序

我们将数组前半部分排好序的称为有序序列，后半部分乱序的称为乱序序列。
初始时有序序列为空，整个数组都为乱序序列。

遍历 n 次数组，每次遍历整个乱序序列，选出乱序序列中最小值；遍历结束后将该最小值添加在有序序列后一位上。

void SelectSort(int arr[], int len)
{
	//最小元素索引
	int min;
	for (int i = 0; i < len - 1; ++i)
	{
		//最小元素首先等于当前元素，（索引）
		min = i;
		for (int j = i+1; j < len; ++j)
		{
			if (arr[j] < arr[min])
			{
				min = j;
			}
		}
		swap(arr[i], arr[min]);
	}
}

• 外层循环 i 的值表示当前乱序序列首位元素的下标，在选出乱序序列中的最小值后，要将最小值放到 i 的位置
• 1个数不能比较大小，因此我们将 min 初始化为 i ，将它与其后面的元素比较；因此内层循环 j 的初始值为 i + 1
• 因为 j 的初始值为 i + 1 ，为了防止数组越界，外层循环跳出条件要多减1

---

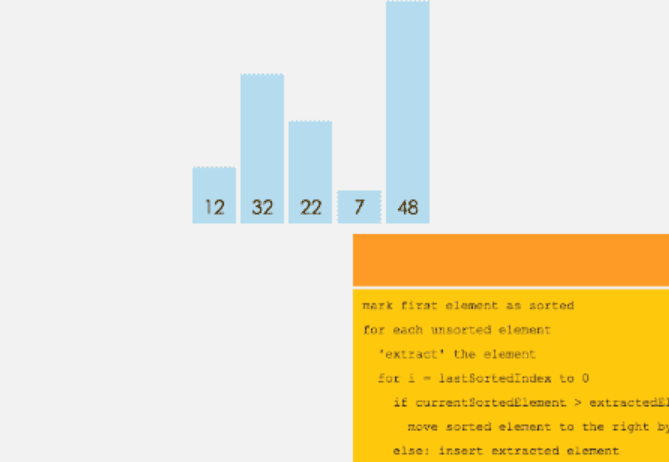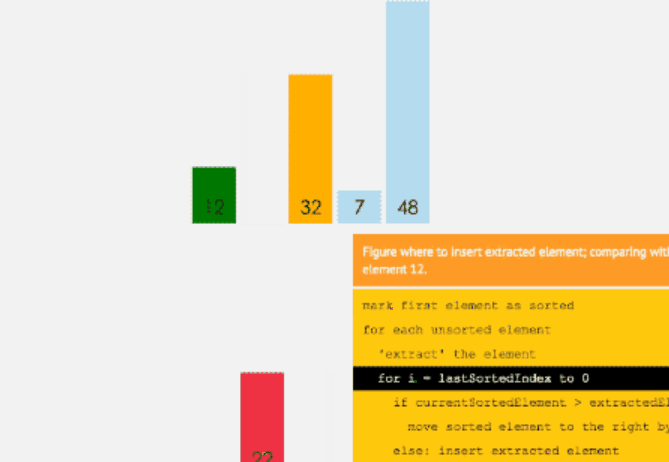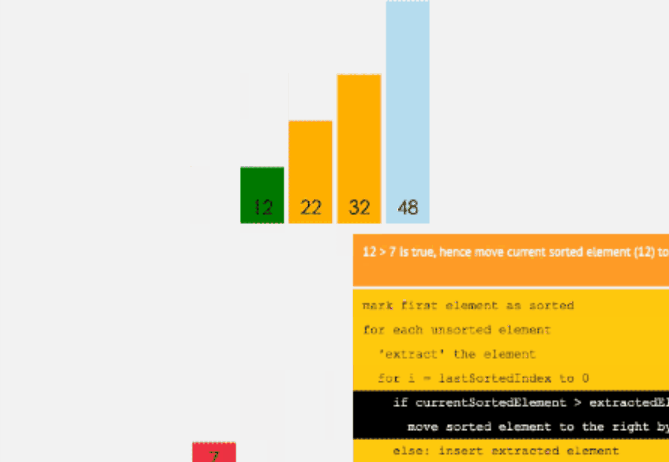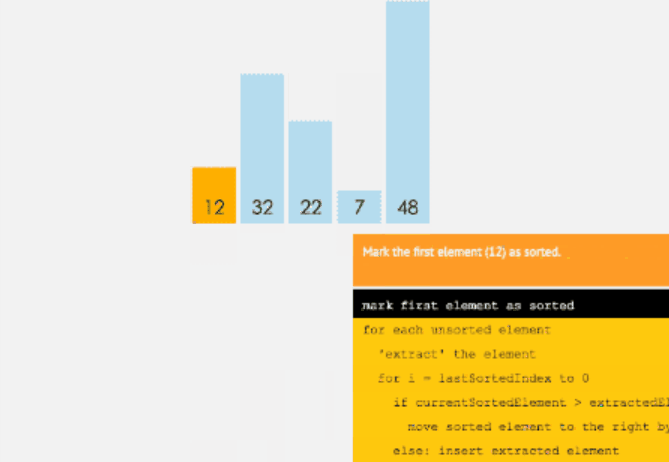
插入排序

和选择排序一样，我们将数组前面部分排好序的称为有序序列，右面部分乱序的称为乱序序列。
初始时有序序列有1个元素，即数组的第一位元素，其余的为乱序序列。

如果将选择排序看作是“选择合适元素放入指定位置”，那么插入排序就是“选择合适位置插入元素”。
遍历 n 次数组（ n 为乱序序列元素个数），每次遍历整个有序序列；将乱序序列第一个元素放进有序序列，并且有序序列仍为有序。

void InsertSort(int arr[], int len)
{
	for (int i = 1; i < len; ++i)
	{
		int j;
		int temp = arr[i];
		for (j = i-1; j>=0; --j)
		{
			if (arr[j] > temp)
			{
				arr[j + 1] = arr[j];
			}
			else
				break;
		}
		//跳出后，j+1指向的是temp要插入的位置
		arr[j + 1] = temp;
	}
}

• 外层循环从乱序序列第一位开始向后遍历，因此 i = 1；i < len
• 内层循环从有序序列最后一位开始向前遍历，因此 j =  i – 1；j >= 0
• a[i] 变量为我们要插入的元素，为了防止内层循环将它覆盖，我们用 temp 暂时存储
• 当 j 指向的元素大于 temp的值时，我们将 j 指向的元素向后移动一格，让出插入位置；否则说明当前 j 的位置就是要插入的位置，因此执行 break 语句
• 因为执行 break 语句之前，执行过 j– 语句，因此跳出内层循环后，真正的插入位置为 j + 1；（或者可以理解为，插入位置为当前遍历到的有序序列元素的后面一个位置）

---

快速排序

快速排序，包括后面的归并排序时分治思想的经典例子。
快速排序中，将数组划分和算法分开，不论是从程序设计的角度还是增强代码可读性的角度来看，它的精妙之处值得反复品味。

快速排序，初始时整个数组都是乱序的，这时我们运用一个“算法”，将数组重新排列成如 [ 比中间值小的序列 – 中间值 – 比中间值大的序列] 的样子；其中前后子序列可以是乱序的（一般总是乱序的）。

那么那个“算法”是什么呢？很简单，选出一个主元作为中间值（一般选择数组第一位元素为主元），然后遍历数组，将比主元小的数放在它的左边，将比主元大的（或比等于主元）数放在它的右边；然后对左右两个序列再次执行该算法，直到子序列只有一个元素时跳出。

下图中，黄色的元素为主元，红色为比主元小的元素，紫色为比主元大的元素。

void QuickSort(int arr[], int l, int r)
{
	if (l < r)
	{
		int m = QuickSortPartition(arr, l, r);
		QuickSort(arr, l, m - 1);
		QuickSort(arr, m + 1, r);
	}
}

int QuickSortPartition(int arr[], int l, int r)
{
	int swapIndex = l;//用于交换元素
	int x = arr[l];//主元
	for (int i = l + 1; i <= r; ++i)//注意i的初值不要设置成0和上边界
	{
		if (arr[i] < x)
		{
			swap(arr[i], arr[swapIndex + 1]);
			swapIndex++;
		}
	}
	//跳出循环后，swapIndex指向的是左序列最后一位元素
	swap(arr[l], arr[swapIndex]);
	//交换后，swapIndex指向的是主元
	//此时，主元左边的元素都小于它，右边的元素都大于等于它
	return swapIndex;
}

• QuickSort为外部调用的函数，它调用“算法”，并对数组进行划分
• QuickSortPartition为“算法”部分，将划分好的数组排列成 小 – 中 – 大 的样子，并返回主元的索引值，让QuickSort函数根据主元索引值来划分数组
• 注意，两个函数的的参数列表中，l 和 r 分别表示数组的左右范围索引，r 不是数组元素个数

---

归并排序

在代码结构上归并排序与快速排序比较类似，但它们的核心思路不太一样——
快速排序是从完整的数组开始执行“算法”，然后划分出子序列再执行“算法”，是从整体到局部的路线；
但归并排序是一开始就向下划分到最小序列A（只有一个元素），并将序列A1和A2排好序，组合成新的序列，然后再回到比刚才序列大一级的序列B中，并将B1和B2也排好序组合成新序列，重复执行该步骤，直到整个数组都排好序。因此归并排序体现的是从局部到整体的路线。

那么如何实现一开始向下划分，然后又原路返回的功能呢？用递归！这也是归并排序名字的由来——递归下去，合并上来。

从上图中可以看出，归并排序需要一个额外的临时数组（图的下半部分），用于将两个序列合并起来，再将临时数组的元素赋给原数组。

这将多花费 O(n) 的空间复杂度，比快速排序的 O(log₂n) 要差一些；但比快速排序优秀一点的是，归并排序不会出现时间复杂度最差为 O(n²) 的情况，它的平均时间性能要好于快速排序。

void MergeSort(int arr[], int l, int r, int temp[])
{
	if (l < r)
	{
		int m = (l + r) / 2;
		MergeSort(arr, l, m, temp);
		MergeSort(arr, m + 1, r, temp);
		MergePartition(arr, l, r, m, temp);
	}
}

void MergePartition(int arr[], int l, int r, int m, int temp[])
{
	//左右序列指针
	int i = l, j = m + 1;
	//temp数组指针
	int t = 0;
	//在左右序列中，将当前指针指向的较小元素放进temp数组
	while (i <= m && j <= r)
	{
		if (arr[i] < arr[j])
		{
			temp[t++] = arr[i++];
		}
		else
		{
			temp[t++] = arr[j++];
		}
	}
	//出来后，将可能剩下的元素全部放进temp数组
	while (i <= m)
	{
		temp[t++] = arr[i++];
	}
	while (j<=r)
	{
		temp[t++] = arr[j++];
	}

	//将temp数组的元素誊到arr数组里
	t = 0;
	while (l <= r)
	{
		arr[l++] = temp[t++];
	}
}

• 外部调用的是MergeSort函数，实现划分序列和调用MergeSortPartition来执行“算法”。从这里就能看出与快速排序的区别——归并排序先划分，再执行算法，而快速排序是反过来的
• 两个函数的参数列表中的 l 和 r 与快速排序中的一样，都是（子）数组的左右索引

---