面试题53 – I. 在排序数组中查找数字 I
统计一个数字在排序数组中出现的次数。

思路:先用二分法查找target,然后查找target前面和后面的相同的值。
class Solution {
public:
int search(vector<int>& nums, int target)
{
if(nums.empty())
return 0;
int i=0,j=nums.size()-1;
int count=0,index,temp;
while(i<=j)
{
int m = (i+j) / 2;
if(nums[m]==target)
{
index = m;
temp = m;
count++;
break;
}
else if(nums[m] < target)
i = m + 1;
else if(nums[m] > target)
j = m - 1;
}
while(index < nums.size()-1)
{
index++;
if(nums[index]==target)
count++;
else
break;
}
index = temp;
while(index > 0)
{
index--;
if(nums[index]==target)
count++;
else
break;
}
return count;
}
};
面试题53 – II. 0~n-1中缺失的数字
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。

以0开头的升序数组nums,若每个元素都递增1,i为数组nums的下标,则i=nums[i]。
知道了这个特性,我们便可以从头遍历数组,判断当前是否 i = nums[i]
若 i ≠ nums[i],则找到了缺失数字,返回 i 即可。
但递增排序数组的查找题,一般可以用二分查找来降低时间复杂度。
思路:二分查找
我们将数组分为两部分:左子数组和右子数组
左子数组:i = nums[i]
右子数组:i ≠ nums[i]
缺失的数字等于“右子数组的首位元素”对应的索引
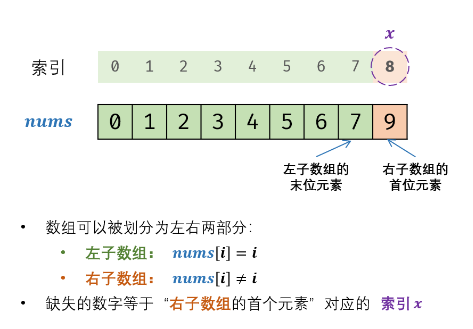
- 左边界 i = 0,右边界 j = nums.size();
- 当 i ≤ j 时循环,即当闭区间[i,j]为空时跳出;
- 计算中点 m = (i+j) / 2;
- 若 i = nums[i] ,则 右子数组的首位元素 一定在闭区间 [m+1,j] 中,因此执行 i=m+1;
- 若 i ≠ nums[i] ,则 左子数组的末位元素 一定在闭区间 [i,m-1] 中,因此执行 j=m-1;
- 跳出时,i 和 j分别指向 右子数组首位元素和 左子数组首位元素。返回 i 。
class Solution {
public:
int missingNumber(vector<int>& nums)
{
int i=0,j=nums.size()-1;
int m;
while(i<=j)
{
m = (i + j) / 2;
if(m == nums[m])
i = m + 1;
else
j = m - 1;
}
return i;
}
};
面试题54. 二叉搜索树的第k大节点
给定一棵二叉搜索树,请找出其中第k大的节点。

- 在 面试题36. 二叉搜索树与双向链表 中,我们知道二叉搜索树的中序遍历序列是递增的,我们可以在中序遍历中找到二叉搜索树的第 k 小节点。
- 该题求二叉搜索树的第 k 大节点,那么我们可以反着中序遍历,即遍历顺序为 [右子树 | 根 | 左子树] ,得到的为降序序列。
- 我们用 全局变量count 来表示遍历过节点的个数,初始值为 k ;每遍历一个节点, count– ,当 count = 0 时表示我们找到了目标节点。
- 用 全局变量res 来存储返回值,当 count = 0 时,将节点的 val 存进 res 。
- count = 0 后,后面的递归遍历将没有意义,于是在 count = 0 后,直接返回,不再递归遍历。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int count,res;
int kthLargest(TreeNode* root, int k)
{
count = k;
dfs(root);
return res;
}
void dfs(TreeNode *node)
{
if(node == nullptr || count == 0)
{
return;
}
dfs(node->right);
count--;
if(count == 0)
{
res = node->val;
return;
}
dfs(node->left);
}
};
面试题55 – I. 二叉树的深度
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7] ,

返回它的最大深度 3 。
提示:节点总数 <= 10000
思路:深度优先搜索,先序遍历
- 申请变量 currentDepth=0 ,记录当前遍历到节点的深度,每向下遍历一个节点则 +1 ;遍历到叶子节点后返回前 -1 。
- 申请变量 resDepth ,从叶子节点返回前,且在 currentDepth 值 -1 前,执行 resDepth = max(resDepth,currentDepth); ,记录当前最长深度,当遍历完二叉树后,resDepth保存的是树的最深深度。
- 最后返回 resDepth 。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int currentDepth=0;
int resDepth;
int maxDepth(TreeNode* root)
{
if(root == nullptr)
return 0;
dfs(root);
return resDepth;
}
void dfs(TreeNode *node)
{
if(node == nullptr)
return;
currentDepth++;
dfs(node->left);
dfs(node->right);
//此时从叶子节点返回
resDepth=max(resDepth,currentDepth);
currentDepth--;
}
};
思路二:后序遍历
树的深度 = max(左子树深度,右子树深度) + 1;
class Solution {
public:
int maxDepth(TreeNode* root)
{
if(root == nullptr)
return 0;
return max(maxDepth(root->left),maxDepth(root->right)) +1;
}
};
面试题55 – II. 平衡二叉树
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。

思路一:后序遍历,自底向上,本题的最优解
- 由后序遍历的性质可知,当检查到节点A时,其左子树与右子树也已经检查过了,因此我们只需要比较其左右子树的深度是否 ≤ 1 即可:若深度 ≤ 1 ,则返回当前子树的深度,否则返回 -1 ,表示子树不平衡。
- 如何计算子树的深度:当前子树根节点的左子树深度与右子树深度的最大值+1 ;若根节点为空,则深度为0 。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root)
{
if(dfs(root) != -1)
return true;
else
return false;
}
int dfs(TreeNode *node)
{
if(node == nullptr)
return 0;
int leftDepth = dfs(node->left);
//剪枝
if(leftDepth == -1)
return -1;
int rightDepth = dfs(node->right);
//剪枝
if(rightDepth == -1)
return -1;
if(abs(leftDepth - rightDepth)<=1)
return max(leftDepth,rightDepth) + 1;
else
return -1;
}
};
思路二:前序遍历,自顶向下,时间复杂度较高
前序遍历的中心思想与上一题“二叉树的深度”类似,就是计算每棵子树的深度。
class Solution {
public:
bool isBalanced(TreeNode* root)
{
if(root == nullptr)
return true;
return abs(dfs(root->left) - dfs(root->right))<=1 && isBalanced(root->left) && isBalanced(root->right);
}
int dfs(TreeNode *node)
{
if(node == nullptr)
return 0;
return max(dfs(node->left),dfs(node->right)) +1;
}
};
面试题56 – I. 数组中数字出现的次数
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。

最直观的方法是用哈希表
class Solution {
public:
vector<int> singleNumbers(vector<int>& nums)
{
unordered_map<int,int> mp;
vector<int> res;
for(auto n:nums)
mp[n]++;
for(auto n:nums)
{
if(mp[n]==1)
res.push_back(n);
}
return res;
}
};
但题目要求时间复杂度是O(n),空间复杂度是O(1)
思路:分组位运算,异或运算(题解方法来自leetCode题解——eddie也有大厂梦大佬)
由于数组中存在着两个数字不重复的情况,我们将所有的数字异或操作起来,最终得到的结果是这两个数字的异或结果:(相同的两个数字相互异或,值为0) 最后结果一定不为0,因为有两个数字不重复。
插一句:如果题目简单点改成只有一个数字不重复,那样我们直接将所有数字异或运算起来,最后的结果就是只出现一次的数字。
举例:

此时我们无法通过 111(二进制),去获得 110 和 001。
那么当我们可以把数组分为两组进行异或,那么就可以知道是哪两个数字不同了。
我们可以想一下如何分组:
- 重复的数字进行分组,很简单,只需要有一个统一的规则,就可以把相同的数字分到同一组了。例如:奇偶分组。因为重复的数字,数值都是一样的,所以一定会分到同一组!
- 此时的难点在于,对两个不同数字的分组。
此时我们要找到一个操作,让两个数字进行这个操作后,分为两组。
我们最容易想到的就是 & 1 操作, 当我们对奇偶分组时,容易地想到 & 1,即用于判断最后一位二进制是否为 1。来辨别奇偶。
你看,通过 & 运算来判断一位数字不同即可分为两组,那么我们随便两个不同的数字至少也有一位不同吧!
我们只需要找出那位不同的数字mask,即可完成分组( & mask )操作。
由于两个数异或的结果就是两个数数位不同结果的直观表现,所以我们可以通过异或后的结果去找 mask!
所有的可行 mask 个数,都与异或后1的位数有关。

为了操作方便,我们只去找最低位的mask
class Solution {
public:
vector<int> singleNumbers(vector<int>& nums)
{
//将所有数异或起来
int k=0;
for(auto n:nums)
k ^= n;
//获取k中最低位的1
int mask=1;
while((k & mask)==0)
mask <<=1;
//将nums分成a、b两组
int a=0,b=0;
for(auto n:nums)
{
if((n & mask)==0) //mask位为0
a ^= n;
else //mask位为1
b ^= n;
}
vector<int> res{a,b};
return res;
}
};
面试题56 – II. 数组中数字出现的次数 II
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。

最佳题解涉及到有限状态自动机,我还是用哈希表吧ORZ
class Solution {
public:
int singleNumber(vector<int>& nums)
{
int res;
unordered_map<int,int> mp;
for(auto n:nums)
mp[n]++;
for(auto n:nums)
if(mp[n] == 1)
res = n;
return res;
}
};
面试题57. 和为s的两个数字
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。

这道题可以用哈希表、二分查找和双指针做。
思路:双指针
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target)
{
int l=0,r=nums.size()-1;
vector<int> ans;
while(l<r)
{
int res = nums[l]+nums[r];
if(res == target)
{
ans.push_back(nums[l]);
ans.push_back(nums[r]);
return ans;
}
if(res < target)
l++;
if(res > target)
r--;
}
return ans;
}
};
面试题57 – II. 和为s的连续正数序列
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。

思路:双指针(滑动窗口)
变量:指向滑动窗口内最左元素 左指针l ,指向滑动窗口内最右元素 右指针r ,当前滑动窗口内的和 sum 。
算法解析:
-
循环执行下列步骤,当 l ≥ r 时跳出:
-
计算滑动窗口内的 sum,可由等差数列求和公式Sn=n(a1+an)/2得出sum=(l+r)*(r-l+1)/2。
-
比较 sum 和 target 值的大小:
-
若sum==target,则该滑动窗口内是我们要找的序列,将它们依次保存进 临时数组temp ,再将temp装进 结果数组res 。每个数字开头的序列,最多只有一项符合要求,因此 左指针l++ ;
-
若sum<target,则说明还需要再往滑动窗口内添加新值,因此 r++ ;
-
若sum>target,则说明当前 l 指针所指向的数字开头的序列没有符合要求的,因此 l++ 。
-
class Solution {
public:
vector<vector<int>> findContinuousSequence(int target)
{
vector<vector<int>> res;
vector<int> temp;
int l=1,r=2,sum;
while(l<r)
{
//等差数列求和公式
sum = (l+r)*(r-l+1)/2;
if(sum == target)
{
temp.clear();
for(int i=l;i<=r;++i)
temp.push_back(i);
res.push_back(temp);
l++;//不要忘了移动左指针
}
else if(sum < target)
r++;
else if(sum > target)
l++;
}
return res;
}
};
面试题58 – I. 翻转单词顺序
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串”I am a student. “,则输出”student. a am I”。

思路:
先不考虑多余空格的问题,要翻转单词顺序,我们可以先翻转每个单词中字符的顺序,得到序列s,然后再翻转序列s中每个字符的顺序。
剩下的就是处理多余空格了。
class Solution {
public:
string reverseWords(string s)
{
if(s.empty()) return "";
int k=0,e=s.size()-1;
while(k<s.size() && s[k]==' ')//消除头部空格
k++;
while(e>=0 && s[e]==' ')//消除尾部空格
e--;
if(k>=s.size() || e<0)//当输入只有空格时
return "";
string temp="",res="";
for(int i=k;i<=e;i++)
{
if(s[i] != ' ')//将单词放入temp
temp += s[i];
else//当遇到单词间的空格时
{
while(s[i] == ' ')//消除单词间多余空格
i++;
i--;//抵消for循环的i++,不然下个单词首字母会被忽略
res += swapstr(temp);//将单词中字母翻转后放入res
res += " ";//加上单词之间的一个空格
temp="";
}
}
//跳出循环后,temp中还有一个单词没有处理
res += swapstr(temp);
//最后将res整体翻转
return swapstr(res);
}
string swapstr(string s)
{
int i=0,j=s.size()-1;
while(i<j)
swap(s[i++],s[j--]);
return s;
}
};
面试题58 – II. 左旋转字符串
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串”abcdefg”和数字2,该函数将返回左旋转两位得到的结果”cdefgab”。

思路一:最直观的方法是拼接两个子字符串
class Solution {
public:
string reverseLeftWords(string s, int n)
{
string res;
for(int i=n;i<s.size();++i)
res += s[i];
for(int i=0;i<n;++i)
res += s[i];
return res;
}
};
思路二:原地交换:块交换
“abcdefg”;先交换前两个:”bacdefg”;再交换剩下的:”bagfedc”;
最后整体交换:”cdefgab”。
class Solution {
public:
string reverseLeftWords(string s, int n)
{
int len = s.size();
for(int i = 0;i < n/ 2;i++)
swap(s[i],s[n - i - 1]);
for(int i = n;i < (len + n) / 2;i++)
swap(s[i],s[len - (i - n) - 1]);
for(int i = 0;i < len / 2;i++)
swap(s[i],s[len - i - 1]);
return s;
}
};
面试题59 – I. 滑动窗口的最大值
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。

提示:
你可以假设 k 总是有效的,在输入数组不为空的情况下,1 ≤ k ≤ 输入数组的大小。
思路一:用双端队列,单调队列
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
vector<int> res;
deque<int> q;
int l=0,r;
if(nums.empty())
return res;
for(r=0;r<k;++r)//还未形成窗口
{
//队列中只保留队首元素和比它小的降序序列
while(!q.empty() && q.back()<nums[r])
q.pop_back();
//窗口中新增元素
q.push_back(nums[r]);
}
//刚刚形成窗口后也要加入res
res.push_back(q.front());
//形成窗口之后
for(r=k;r<nums.size();++r)
{
//如果队首元素已经不在窗口里,出队l
if(!q.empty() && q.front() == nums[l])
q.pop_front();
l++;
//相同的,队列中只保留队首元素和比它小的降序序列
while(!q.empty() && q.back()<nums[r])
q.pop_back();
//窗口中新增元素
q.push_back(nums[r]);
//加入res
res.push_back(q.front());
}
return res;
}
};
思路二:暴力遍历,窗口中每新增和淘汰数后就找出窗口中最大的数。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
vector<int> res;
int l=0,r=k-1;
for(;r<nums.size();++l,++r)
{
int maxNum=nums[l];
for(int i=l+1;i<=r;++i)
{
maxNum=max(maxNum,nums[i]);
}
res.push_back(maxNum);
}
return res;
}
};
面试题59 – II. 队列的最大值
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1


该图来自题解区大佬@支付中心。
class MaxQueue {
public:
queue<int> q;
deque<int> deq;
MaxQueue()
{
}
int max_value()
{
if(deq.empty())
return -1;
return deq.front();
}
void push_back(int value)
{
q.push(value);
while(!deq.empty() && deq.back()<value)
deq.pop_back();
deq.push_back(value);
}
int pop_front()
{
if(q.empty())
return -1;
if(q.front() == deq.front())
{
deq.pop_front();
int res=q.front();
q.pop();
return res;
}
else
{
int res=q.front();
q.pop();
return res;
}
}
};
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue* obj = new MaxQueue();
* int param_1 = obj->max_value();
* obj->push_back(value);
* int param_3 = obj->pop_front();
*/
剑指 Offer 61. 扑克牌中的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。

这道题中的“顺子”,只要数字能连起来就行。数组中的0,即大王小王是万能牌,能变成任意数字来组成顺子。
思路:先不考虑数字0(大小王),若能组成顺子,则最大数减最小数的结果小于5。
那么我们要找到除了0以外的最小数和最大数:先排序。
特别的:如果数组中有重复的数(0除外),则一定不会是顺子。
class Solution {
public:
bool isStraight(vector<int>& nums)
{
sort(nums.begin(),nums.end());
int min=0,max=4;
for(int i=0;i<nums.size();++i)
{
if(nums[i] == 0)
min++;
//除大小王外有重复牌时,没有顺子
else if(i > 0 && nums[i] == nums[i-1])
return false;
}
//如果最大值减最小值小于5,则有顺子,否则没有顺子
if(nums[max] - nums[min]<5)
return true;
return false;
}
};





