面试题31. 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

思路:借用一个辅助栈stack,模拟压入/弹出操作的排列。根据是否模拟成功,即可得到结果。
入栈操作:按照压栈序列的顺序执行。
出栈操作:每次入栈后,循环判断“栈顶元素=弹出序列的当前元素”是否成立,将符合弹出序列顺序的栈顶元素全部弹出。
最后判断出栈列表指针是否指向出栈列表的末尾即可。
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped)
{
if(popped.empty())
{
return true;
}
stack<int> a;
int indexPop=0;
for(int i=0;i<pushed.size();++i)
{
a.push(pushed[i]);
while(!a.empty()&&a.top()==popped[indexPop])//第一个判断非空放在前面
{
a.pop();
indexPop++;
if(indexPop==popped.size())
{
return true;
}
}
}
return false;
}
};
面试题32 – I. 从上到下打印二叉树
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。

class Solution {
public:
vector<int> levelOrder(TreeNode* root)
{
vector<int> res;
if(root==NULL)
{
return res;
}
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
//队首元素出队
TreeNode* node=q.front();
q.pop();
//出队元素加入res
res.push_back(node->val);
//出队元素子结点入队
if(node->left!=NULL)
q.push(node->left);
if(node->right!=NULL)
q.push(node->right);
}
return res;
}
};
面试题32 – II. 从上到下打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。

思路:这个题与普通的二叉树层序遍历的不同点在于,要区分不同层的节点并把同一层的节点打印到一起。
因此我们在原本的循环内再添加一个循环,循环次数为当前队列的长度——跳出循环时就打印完一层节点,并且它们的子结点全部入队。
为了临时存储一层节点的值,我们申请了一个临时列表tem来辅助。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
vector<vector<int>> res;
if(root==NULL)
{
return res;
}
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
vector<int> tem;
int size=q.size();
for(int i=0;i<size;++i)
{
TreeNode* temp=q.front();
q.pop();//执行完这一句会改变q.size()的返回值
tem.push_back(temp->val);
if(temp->left!=NULL)
q.push(temp->left);
if(temp->right!=NULL)
q.push(temp->right);
}
res.push_back(tem);
}
return res;
}
};
面试题32 – III. 从上到下打印二叉树 III
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。

思路:
- 标识值:因为向左向右打印的顺序是每层替换的,所以需要一个bool标识值right,通过它来判断接下来的打印顺序。right为true表示当前为向右打印,为false表示当前为向左打印。
- 辅助队列:和普通的层序遍历一样,需要一个队列来完成BFS搜索。
- 辅助vector:和上题的每层节点打印到一组一样,需要一个辅助vector来暂存同一层的节点值,然后把它加入到结果vector里res。
- 辅助栈:这是这题新添加的辅助栈,仔细想一下,由于当前层和下一层打印顺序是倒序的,因此我们需要借助栈的先入后出的特点:在打印队列节点时,同时将节点入栈保存;当队列节点打印完后(同时队列里已经没有节点),将栈里的节点依次出栈,根据标识值right的布尔值将这些节点的子结点加入队列。
- 子结点入队的顺序:如果下一层是向左打印(right==true),则先加入右节点,再加入左节点;如果下一层是向右打印(right==false),则先加入左节点,再加入右节点。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
vector<vector<int>> res;
if(root==NULL)
{
return res;
}
bool right=true;
stack<TreeNode*> s;
queue<TreeNode*> q;
q.push(root);
while(!q.empty())
{
vector<int> tem;
//打印队列节点
while(!q.empty())
{
//打印
TreeNode* node=q.front();
tem.push_back(node->val);
//出队并入栈
q.pop();
s.push(node);
}
//将栈里的节点的子结点入队
while(!s.empty())
{
if(right)
{
//如果当前是向右打印
//那下一层是向左打印,右节点先入队,左节点后入队
TreeNode* temp=s.top();
if(temp->right!=NULL)
q.push(temp->right);
if(temp->left!=NULL)
q.push(temp->left);
s.pop();
}
if(!right)
{
//如果当前是向左打印
//那下一层是向右打印,左节点先入队,右节点后入队
TreeNode* temp=s.top();
if(temp->left!=NULL)
q.push(temp->left);
if(temp->right!=NULL)
q.push(temp->right);
s.pop();
}
}
right=!right;//记得转向
res.push_back(tem);
}
return res;
}
};
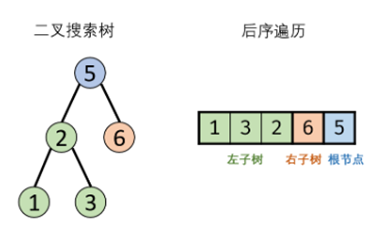
面试题33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:

解题思路:
- 后序遍历定义: [ 左子树 | 右子树 | 根节点 ],即遍历顺序为“左、右、根”。
- 二叉搜索树定义:左子树中所有节点的值<根节点的值;右子树中所有节点的值>根节点的值;其左、右子树也分别为二叉搜索树。
方法:递归分治
- 根据二叉搜索树的定义,可以通过递归,判断所有子树的 正确性 (即其后序遍历是否满足二叉搜索树的定义),若所有子树都正确,则此序列为二叉搜索树的后序遍历。
递归解析:
- 终止条件: 当 i ≥ j ,说明此子树节点数量 ≤ 1,无须判别正确性,因此直接返回true;
- 递推工作:
- 划分左右子数:遍历后序遍历的 [i,j] 区间元素,寻找 第一个大于根节点 的节点,索引记为 m 。此时,可划分处左子树区间 [i,m-1] 、右子树区间 [m,j-1] 、根节点索引 j 。
- 判断是否为二叉搜索树:
- 左子树区间 [i,m-1] 内的所有节点都应 < postorder[j] 。而上面 划分左右子数 步骤已经保证左子树区间的正确性,因此只需要判断右子树区间即可。
- 右子树区间 [m,j-1] 内的所有节点都应 > postorder[j] 。实现方式为遍历,当遇到 ≤ postorder[j] 的节点则跳出;则可通过 p == j 判断是否为二叉搜索树。
- 返回值:所有子树都需正确才可判定正确,因此使用 与逻辑符 && 连接。
- p == j :判断 此树 是否正确。
- recur(i,m-1):判断 此树的左子树 是否正确。
- recur(m,j-1):判断 此树的右子树 是否正确。
复杂度分析:
- 时间复杂度 O(N^2):每次调用 recur(i,j) 减去一个根节点,因此递归占用 O(N);最差情况下(即当树退化为链表),每轮递归都需遍历树所有节点,占用O(N)。
- 空间复杂度 O(N):最差情况下(即当树退化为链表),递归深度将达到 N。
class Solution {
public:
bool verifyPostorder(vector<int>& postorder)
{
return recur(postorder,0,postorder.size()-1);
}
bool recur(vector<int>& postorder,int i,int j)
{
//当只有一个节点,返回true
if(i>=j)
return true;
//p用来寻找子树索引
int p=i;
while(postorder[p]<postorder[j])
p++;
//p停下的地方是右子树开始的索引,用m记录
int m=p;
while(postorder[p]>postorder[j])
p++;
//如果该后续遍历序列正确
//则p应该等于j
//如果该序列正确(p==j),则递归遍历左右子树
return p==j && recur(postorder,i,m-1) && recur(postorder,m,j-1);
}
};
面试题34. 二叉树中和为某一值的路径
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例:
给定如下二叉树,以及目标和 sum = 22,

题目解释:题目给出路径的定义:满足从根节点到叶子节点这一条件,也就是说根节点到中间节点不算一条路径,哪怕它们的val加起来等于sum。
思路:
- 很容易联想到用DFS——从根节点开始搜索到叶子节点,并用临时vector temp记录每个节点的val和它们val的和。(前序遍历)
- 如果val的和与Sum的值相等,则将记录的节点的temp加入进结果vector res。
- 如果搜索到叶子节点,没有找到路径(节点为空),则直接返回。
- 在返回时,temp所记录的最后一个值将作废,所以要将最后一个元素出栈。
关于剪枝:
为什么不能在节点的val和大于Sum后提前返回,提高效率呢?
这是因为没有考虑到有负数的情况,在节点的val和大于Sum后,若后续节点有负数,仍然可以找到路径。
关于递归返回后,节点val和的变化:
我们用变量currentSum来存储节点val和。当我们检查一个节点时,先将它的val值加到currentSum里。然后判断currentSum的值是否与Sum相等,若该结点又恰好是叶子节点,则找到一条路径;若currentSum的值不与Sum相等,它又恰好是叶子节点,这不是我们要找的路径,因此就要返回上一层调用,有的同学可能觉得currentSum的值同样需要我们手动回溯(减去该节点的val),但其实不然,在递归调用函数中,上一层函数的变量都已经保存在栈里,返回后仍然是调用之前的变量值,这里就免去了一些麻烦。
class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int sum)
{
vector<vector<int>> res;
int currentSum=0;
vector<int> temp;
if(root==NULL)
{
return res;
}
dfs(res,temp,root,sum,currentSum);
return res;
}
void dfs(vector<vector<int>>& res,vector<int>& temp,TreeNode* node,int sum,int currentSum)
{
if(node==NULL)
return;
currentSum+=node->val;
temp.push_back(node->val);//入栈
if(currentSum==sum && node->left==NULL && node->right==NULL)//如果找到路径并且是叶子节点
{
res.push_back(temp);//加入结果res
}
dfs(res,temp,node->left,sum,currentSum);
dfs(res,temp,node->right,sum,currentSum);
temp.pop_back();//返回父节点时出栈
}
};
面试题35. 复杂链表的复制
请实现 copyRandomList 函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
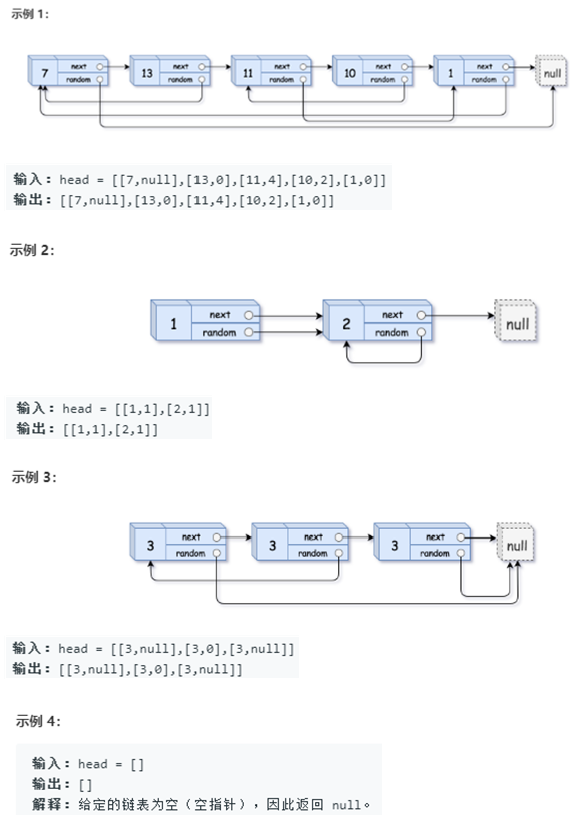
该题难点在于新链表 random 指针的操作。
思路一:用哈希表
先创建新链表,将它们用 next指针 串起来,这一步很好做。
然后配置它们的 random指针 ,如果要把时间复杂度降低到O(N),则需要使用哈希表——创建映射关系为 <旧节点N,新节点N’> 的哈希表,只要我们找到 N 的 random指针 所指向的节点 S ,就能找到 S’,而这个 S’就是 N’的random指针所要指向的 节点 。
同理,在配置random指针之前配置next指针时,也是用同样的方法——找到 N 的 next指针 所指向的节点 S ,也就找到了 S’,将S’赋值给N’的next指针。
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
Node* copyRandomList(Node* head)
{
if(head==NULL)
{
return NULL;
}
//<旧链表节点,新链表节点>对应关系的哈希表
unordered_map<Node*,Node*>mp;
Node* cur=head;
while(cur!=NULL)
{
mp[cur]=new Node(cur->val);
//上一句中,cur是key值,mp[cur]是映射值,建立映射关系
cur=cur->next;
}
cur=head;
while(cur!=NULL)
{
if(cur->next!=NULL)//最后一个节点的next已经是NULL
{
mp[cur]->next=mp[cur->next];
//cur->next是原节点N,mp[cur->next]是新节点N'
//将原节点N的next指针指向的下一个节点S所对应的新结点S',赋值
给原节点N所对应的新节点N'的next指针指向的下一个节点
}
if(cur->random!=NULL)//只用考虑不为NULL的
{
mp[cur]->random=mp[cur->random];
}
cur=cur->next;
}
return mp[head];
}
};
代码中第一个循环是建立 <N,N’> 关系,第二个循环是配置next和random指针。
思路二:在不使用辅助空间的情况下实现O(N)的时间效率。
- 复制节点:将原始链表的任意节点 N 复制为新结点 N’ ,再把 N’ 连接到 N 的后面。即如果原始链表为 A->B->C->D 则复制过后为
A->A’->B->B’->C->C’->D->D’ - 确定每个新节点 N’ 的random指针指向:
显然,如果原始链表上的节点 N 的 random 指针指向节点 S ,则它对应的复制节点 N’ 的 random指针 指向节点 S 的复制节点 S’ ,也就是当前节点 S 的 下一个节点 。 - 拆分链表:
把这个长链表拆分成两个链表,把奇数位置的节点连接起来就是原始链表,把偶数位置的节点连接起来就是复制出来的链表。
注意:此时在得到复制链表的同时,不要忘记将原有链表进行复原。
class Solution {
public:
Node* copyRandomList(Node* head)
{
if(head==NULL)
{
return NULL;
}
Node* cur=head;
while(cur!=NULL)//复制节点
{
Node* temp=new Node(cur->val);
temp->next=cur->next;
cur->next=temp;
cur=cur->next->next;
}
cur=head;
while(cur!=NULL)//配置random指针
{
if(cur->random!=NULL)
cur->next->random=cur->random->next;
cur=cur->next->next;
}
//拆分节点
Node* res=head->next;
Node* tem=head->next;
head->next=head->next->next;//准备工作
head=head->next;
while(head!=NULL)
{
tem->next=head->next;
head->next=head->next->next;
head=head->next;
tem=tem->next;
}
return res;
}
};
面试题36. 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
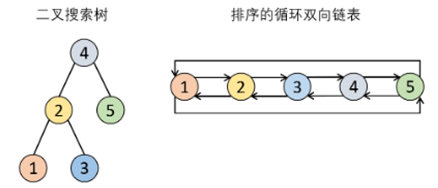
思路:
该题要求将二叉搜索树转换成排序双向链表,通过了解二叉搜索树的性质可知,用中序遍历的方法可以获得排序序列。因此我们将用中序遍历的方法DFS二叉搜索树,同时用一个pre指针来记录,在遍历顺序上,当前节点cur的上一个节点(如cur递归返回到2,pre留在1;cur递归到3,pre留在2),再通过这两个指针来完成链表的构造工作。
细节:
- 如何确定链表头结点:一开始,先申请头指针head,执行DFS,当对节点进行操作时查看pre是否是null,如果是,则说明当前链表为空,该节点是头节点,将其赋值给head;如果不是,则执行正常的链表节点连接工作。
- 如何将头结点和尾节点连接起来:DFS执行完毕后,pre指针指向的是链表的尾节点,通过这个信息,可以对pre指针和head指针进行操作,连接头尾节点。
class Solution {
public:
Node* pre,*head;//前序指针和头指针在两个函数里都会用到,申请为全局变量
Node* treeToDoublyList(Node* root)
{
if(root==NULL)
return NULL;
dfs(root);
//连接头节点和尾节点,最后是pre指针指向尾结点
head->left=pre;
pre->right=head;
return head;
}
void dfs(Node* cur)
{
if(cur==NULL)
return;
dfs(cur->left);//中序遍历,先访问左子树
//返回父节点
if(pre==NULL)//pre为空,说明找到了链表第一个节点
head=cur; //头指针指向第一个节点
else
{
//连接前驱节点和孩子节点
pre->right=cur;
cur->left=pre;
}
pre=cur;//前序指针移动到cur指针上做记录
dfs(cur->right);//访问右子树
}
};
面试题38. 字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
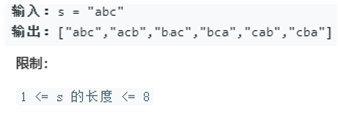
思路:DFS回溯
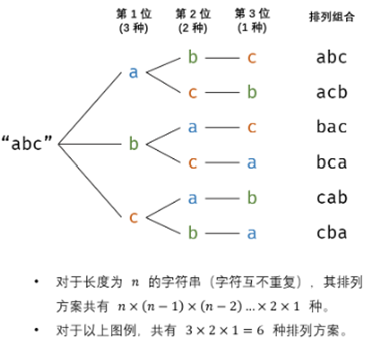
示例中的字符串“abc”,如果看做树,能够很好理解用DFS解决:当确定一个根节点a,那么将分出两条路(只剩下两个字符)b、c,然后向下递归,再确定一个根节点b或者c,再次分路,以此类推。
我们可以通过 字符交换 ,先固定第1位字符(n种情况)、再固定第2位字符(n-1种情况)、……、最后固定第n位字符(1种情况)。
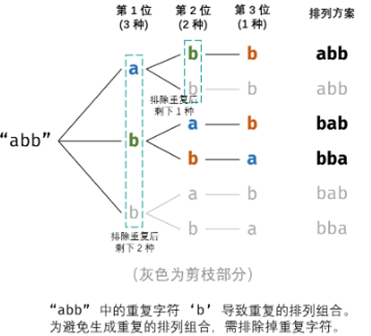
重复方案与剪枝:当字符串存在重复字符时,排列方案中也存在重复方案。为排除重复方案,需在固定某位字符时,保证“每种字符只在此位固定一次”,即遇到重复字符时不交换,直接跳过。从DFS角度看,此操作称为“剪枝”。
递归解析:
- 终止条件:当固定位索引 x = 字符串最后一位索引 时,则将当前组合加入结果。
- 递推参数:当前固定位 x 。
- 递推工作:初始化一个 set ,用于排除重复的字符;将第 x 位字符与
i∈[x,len(字符串)]字符分别交换,并进入下层递归(分路);- 剪枝:若当前字符在 set 中,代表其是重复字符,因此剪枝。
- 将当前字符加入 set ,以便之后对重复字符剪枝。
- 固定字符:将字符 [x] 和 [i] 交换,即固定 [i] 为当前为字符。
- 开启下层递归:调用dfs(x+1),即开始固定第 x+1 个字符。
- 还原交换:递归返回后,将字符[i]和[x]交换,还原之前的交换
class Solution {
public:
vector<string> res;//结果vector,定义在函数外方便两个函数使用
string c;//s的拷贝,也是为了方便函数使用,减少dfs参数
vector<string> permutation(string s)
{
if(s.empty())
return res;
//将字符串s拷贝给c
c=s;
dfs(0);
return res;
}
//x为当前固定字符的索引
void dfs(int x)
{
//如果已经到最后一个字符了,将结果保存进res
if(x==c.size()-1)
{
res.push_back(c);
return;
}
//不是最后一个字符的话,准备set,辅助剪枝
set<char> char_set;
//这里就很巧妙了,第一层可以是a,b,c那么就有三种情况,这里i = x,正巧dfs(0),正好i = 0开始
// 当第二层只有两种情况,dfs(1)i = 1开始
for(int i=x;i<c.size();++i)
{
//如果已经是重复的字符,剪枝
if(char_set.count(c[i])==1)
continue;
//不是的话,添加进set
char_set.insert(c[i]);
//将c[i]与c[x]交换,实现分路
//这里很是巧妙,当在第二层dfs(1),x = 1,那么i = 1或者 2, 要不是交换1和1,要不交换1和2
swap(c[i],c[x]);
//分路后,向下递归
dfs(x+1);
//递归返回后,恢复交换
swap(c[i],c[x]);
//返回时交换回来,这样保证到达第1层的时候,一直都是abc。这里捋顺一下,开始一直都是abc,那么第一位置总共就3个位置
//分别是a与a交换,这个就相当于 x = 0, i = 0;
// a与b交换 x = 0, i = 1;
// a与c交换 x = 0, i = 2;
//就相当于上图中开始的三条路径
//第一个元素固定后,每个引出两条路径,
// b与b交换 x = 1, i = 1;
// b与c交换 x = 1, i = 2;
//所以,结合上图,在每条路径上标注上i的值,就会非常容易好理解了
}
}
};